Rachunek odmian

1. Reklama

OBLICZANIE ZMIENNE, gałąź matematyki, w której badane są zagadnienia związane z ekstremami integralnych funkcjonałów specjalnego typu. W najprostszym przypadku są to funkcjonale formy.

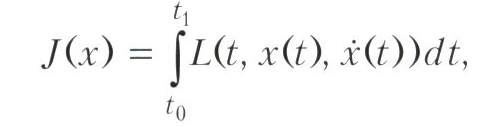
gdzie L = L (t, x, y) jest funkcją trzech zmiennych (zwanych integrandem).

Tutaj x = x (t), y = y (t) są funkcjami zmiennej t, t0≤t≤t1 ,? X (t) jest pochodną funkcji x (t). Zatem wartości argumentu funkcjonalnego J są funkcjami x jednej zmiennej, tj. Rachunku wariacyjnego, części analizy nieskończonej wymiaru, która otrzymała nazwę analizy funkcjonalnej w XX wieku. Z drugiej strony rachunek wariacyjny jest częścią teorii problemów ekstremalnych.

Pierwsze zadania rachunku wariacyjnego. Z historycznego punktu widzenia pierwszym zadaniem rachunku wariacyjnego był problem brachistochronowy, który polega na znalezieniu najbardziej stromej krzywej zniżania łączącej dwa podane punkty (innymi słowy, znalezieniu formy rowu łączącego dwa punkty, opadającej wzdłuż której bez tarcia pod działaniem grawitacji, ciało kończy ruch najkrótszy czas). Problem brachistochrony można sformułować jako problem rachunku wariacyjnego minimalizacji całki

Reklama

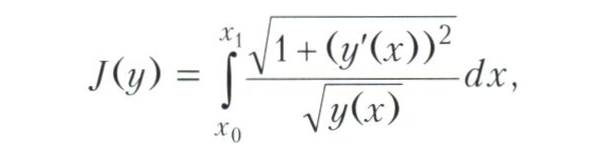
gdzie y (x) jest kształtem rynny i (x0, y (x0)), (x1, y (x1)) są stałymi punktami początkowymi i końcowymi rynny. Zadanie to zaproponował I. Bernoulli w 1696 r. Jako wyzwanie dla matematyków (ogłosił, że zna jej rozwiązanie). Wezwanie zostało przyjęte, a zadanie rozwiązali najwięksi ówczesni naukowcy - J. Bernoulli, G. Leibniz, francuski naukowiec G. Lopital i I. Newton. Decyzje te nakreśliły wiele obszarów przyszłej teorii ogólnej. I. Bernoulli przystąpił do analogii optomechanicznej, J. Bernoulli zastosował zasadę Huygensa (patrz zasada Huygensa-Fresnela), Leibniz rozwiązał problem, zastępując krzywą liniami przerywanymi, kładąc tym samym podwaliny pod metody bezpośrednie w rachunku wariacyjnym.

W rachunku wariacyjnym znajdują się sekcje poświęcone warunkom koniecznym dla ekstremum, warunkom wystarczającym dla ekstremum, pytaniom o istnienie ekstremum oraz algorytmom znajdowania rozwiązań.

Niezbędne warunki dla ekstremum . Sekcje poświęcone warunkom koniecznym dla ekstremum (i wystarczające warunki dla ekstremum) rozwinęły w XVIII wieku L. Euler, J. Lagrange i A. Legendre. Od lat trzydziestych XVIII wieku Euler pracuje nad problemem warunków ekstremalnych w problemach rachunku wariacyjnego. Taki warunek dla najprostszych problemów rachunku wariacyjnego (najprostszy jest problem skrajności funkcjonałów J w ustalonych warunkach brzegowych) okazał się wykonalny na krzywej x, podejrzewanej o ekstremum, równania różniczkowego drugiego rzędu

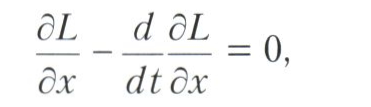
zwane równaniem Eulera. W ważnym szczególnym przypadku (jest on związany z tak zwanym oscylatorem harmonicznym), gdy L = mx2 - kx2, równanie Eulera przyjmuje postać

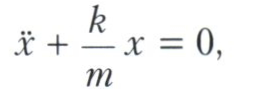
a warunki brzegowe, ogólnie mówiąc, pozwalają nam jednoznacznie określić sinusoidę (rozwiązanie tego równania) łączącą dwa podane punkty określone przez warunki brzegowe. Krzywe, które spełniają równanie Eulera, nazywane są ekstremami, a równanie Eulera nazywane jest stanem stacjonarności. L. Euler wyprowadził to równanie metodą bezpośrednią, zastępując krzywą polilinią, czyli redukując problem do skończonego wymiaru (z późniejszym przejściem do granicy).

L. Euler jako pierwszy rozważył problemy z ograniczeniami, a mianowicie problemy izoperymetryczne, kiedy integralna J jest zminimalizowany, pod warunkiem, że niektóre inne całki przyjmują podane wartości. Klasyczny problem izoperymetryczny polega na maksymalizacji obszaru ograniczonego krzywą o określonej długości. Metody opracowane przez Eulera umożliwiły jednolite rozwiązanie szeregu problemów interesujących dla nauk przyrodniczych i geometrii. Wśród nich są problemy zwiotczenia ciężkich nici, minimalna powierzchnia rewolucji, a także różne warianty klasycznego problemu izoperymetrycznego. Osiągnięcia rachunku wariacyjnego doprowadziły do ​​zrozumienia, że ​​może on służyć jako język nauk przyrodniczych, ponieważ wiele praw natury można sformułować za pomocą zasad wariacyjnych (patrz Zasada możliwych przemieszczeń, Zasada najmniejszego działania).

W 1755 r. J. Lagrange rozpoczął pracę nad rachunkiem wariacyjnym. Zaproponował nowe podejście do badania właściwości krzywych ekstremalnych, oparte na zmienności krzywej podejrzewanej o ekstremum, i podkreślenie głównej liniowej części przyrostu funkcjonalnego, to znaczy, że krzywa podejrzewana o ekstremum ulega małym zmianom, zmienia się, a kwestia przyrostu funkcjonalnego związana z taka odmiana.

Później L. Euler zajmował się również tymi zagadnieniami, który w swojej pracy „Elementy rachunku wariacji” (1764) wprowadził terminy „wariacja” i „rachunek wariacyjny”. W przypadku wielowymiarowych problemów rachunku różniczkowego z wykorzystaniem metody wariacyjnej analogi równania Eulera zostały uzyskane w pierwszej połowie XIX wieku przez K. Gaussa i M. V. Ostrogradskiego.

J. Lagrange badał problemy rachunku wariacyjnego z ograniczeniami o różnym charakterze. W przypadku problemów ze znalezieniem ekstrema funkcji kilku zmiennych z ograniczeniami typu równości zaczął on stosować ogólną technikę, zwaną metodą mnożników Lagrange'a (patrz funkcja Lagrange'a). Lagrange zastosował podobne techniki w problemach rachunku wariacyjnego. Metoda mnożników Lagrange'a pozwala na jednoznaczne wypisanie warunków koniecznych dla ekstremum w różnych problemach rachunku wariacyjnego.

Wystarczające warunki dla ekstremum . Kwestia warunków wystarczających w rachunku wariacyjnym została po raz pierwszy zbadana przez I. Bernoulliego, ale jego praca (1718) pozostała nieznana aż do XX wieku. W 1786 r. A. Legendre znalazł warunek konieczny dla ekstremalności krzywej, polegający na tym, że druga odmiana d2L / d (x?) 2 jest nieujemna (konieczny warunek Legendre'a). Hipoteza, że ​​warunkiem wystarczającym dla ekstremum jest dodatniość drugiej wariacji (ulepszony warunek Legendre) okazała się niepoprawna.

Problem dostateczności słabego ekstremum (gdy powinowactwo mierzy się nie tylko samych funkcji, ale także ich pochodnych) rozwiązał K. Jacobi, opierając się na ideach W. Hamiltona, który wykorzystał je do rozwiązywania problemów mechaniki i optyki. Jacobi wykazał, że warunki lokalne, tj. Warunki sprawdzone w poszczególnych punktach (takie jak równanie Eulera i warunek Legendre'a) nie mogą być wystarczające dla ekstremalności krzywej.

K. Jacobi wprowadził pojęcie sprzężonego punktu ekstremalnego problemu wariacyjnego. Dla najprostszego problemu rachunku wariacyjnego punkt sprzężony ma proste znaczenie geometryczne: jest to punkt przecięcia z ekstremalną obwiednią rodziny ekstremów, które mają wspólny punkt początkowy. Brak punktu sprzężonego w przedziale od punktu początkowego do końcowego jest warunkiem koniecznym dla słabego minimum (warunek konieczny dla Jacobiego). Brak punktu sprzężonego w pół-przedziale od punktu początkowego do punktu końcowego, w tym ostatniego (ulepszony warunek Jacobiego), wraz z równaniem Eulera i rozszerzonym warunkiem Legendre'a, jest wystarczający dla słabego minimum ekstremalnego.

W XIX wieku W. Hamiltonowi udało się zbudować, wychodząc z zasady Huygensa, teorię zjawisk optycznych, a K. Jacobi przeniósł te koncepcje Hamiltona na ogólne problemy rachunku wariacyjnego, co doprowadziło do stworzenia teorii Hamiltona-Jacobiego. W tej teorii bada się wiązki ekstremów, podobne do wiązek promieni i analogów frontów falowych w problemach optyki. Funkcje generujące powstające w tych problemach spełniają równania różniczkowe cząstkowe, które nazywane są równaniami Hamiltona - Jacobiego. Rozwiązanie tych równań daje nowe podejście do rozwiązywania problemów rachunku różniczkowego. Dzięki takiemu podejściu K. Weierstrass w latach 80. XIX wieku znalazł warunki dla silnego minimum (przy uwzględnieniu bliskości tylko współrzędnych fazy).

Rozwiązanie problemów związanych z dostatecznymi warunkami w problemach z ograniczeniami zostało zakończone dopiero w połowie XX wieku, kiedy nowa sekcja teorii ekstremalnych problemów zaczęła nabierać kształtu, zwana teorią optymalnej kontroli. Zadania optymalnej kontroli nazywane są problemami rachunku różniczkowego z dodatkowymi warunkami dla zmiennych (takich jak nierówności i inkluzje), które odzwierciedlają ograniczone możliwości wpływu na kontrolowane procesy. Podstawowe znaczenie w teorii optymalnej kontroli Pontryagin ma maksymalną zasadę; niezbędne warunki Eulera, Legendre'a, Jacobiego i Weierstrassa są konsekwencją zasady maksymalnej.

Stworzenie analizy funkcjonalnej w XX wieku umożliwiło uwzględnienie rachunku wariacji i optymalnej kontroli jako części tej gałęzi matematyki.

Istnienie ekstremum . Teoria istnienia rozwiązań problemów rachunku wariacyjnego powstała w XX wieku. Podstawy tej teorii opierają się również na ogólnych koncepcjach analizy funkcjonalnej.

Algorytmy wyszukiwania rozwiązań. Algorytmy do rozwiązywania problemów rachunku różniczkowego opierają się na dobrych pomysłach, metodach bezpośrednich zastępujących problem skończonych wymiarów oraz metodach rozwiązywania równań pochodzących z niezbędnych warunków ekstremalnych.

Oświetlone: ​​Gelfand I.M., Fomin S.V. Wariacyjny rachunek różniczkowy. M., 1961; Alekseev V.M., Tikhomirov V.M., Fomin S.V. Optymalna kontrola. M., 1979; Buslaev V.S. Wykłady z rachunku wariacyjnego. L., 1980; F. P. Vasiliev Metody optymalizacji. M., 2002.

V. M. Tikhomirov.