варіаційне числення

1. Реклама

Варіаційне числення, розділ математики, в якому вивчаються питання, пов'язані з екстремумами інтегральних функціоналів спеціального виду. У найпростішому випадку це функціонали виду

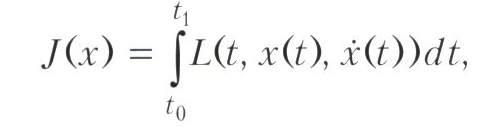
де L = L (t, х, у) - функція трьох змінних (звана інтегрантом).

Тут х = х (t), у = у (t) - функції змінної t, t0≤t≤t1,? X (t) - похідна функції х (t). Таким чином, значеннями аргументу функціонала J є функції х одного змінного, т. Е. Варіаційне числення - розділ бесконечномерного аналізу, який отримав в 20 столітті назва функціонального аналізу. З іншого боку, варіаційне числення є розділом теорії екстремальних задач.

Перші завдання варіаційного обчислення. Історично першим завданням варіаційного обчислення була задача про Брахістохрона, що складається в знаходженні кривої найшвидшого спуску, що з'єднує дві задані точки (або, інакше кажучи, в знаходженні форми жолоба, що з'єднує дві точки, спускаючись по якому без тертя під дією сили тяжіння, тіло завершує рух за найкоротший час). Завдання про Брахістохрона можна сформулювати як задачу варіаційного обчислення про мінімізацію інтеграла

Реклама

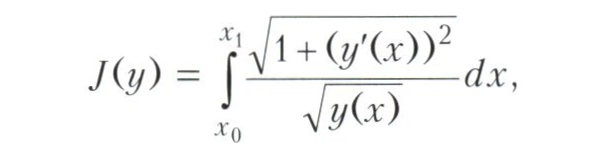
де у (х) - форма жолоба і (х0, у (х0)), (х1, у (х1)) - закріплені початкова і кінцева точки жолоба. Це завдання було запропоновано І. Бернуллі в 1696 році як виклик математикам (він оголосив, що знає її рішення). Виклик був прийнятий, і завдання було вирішено найбільшими вченими того часу - Я. Бернуллі, Г. Лейбніцем, французьким ученим Г. Лопиталем і І. Ньютоном. Ці рішення намітили багато напрямків майбутньої загальної теорії. І. Бернуллі виходив з оптико-механічною аналогією, Я. Бернуллі застосував принцип Гюйгенса (дивись Гюйгенса - Френеля принцип), Лейбніц вирішив задачу, замінюючи криву ламаними, заклавши тим самим основу прямих методів у варіаційному численні.

У варіаційному численні можна виділити розділи, присвячені необхідним умовам екстремуму, достатніх умов екстремуму, питанням існування екстремуму і алгоритмам пошуку рішень.

Необхідні умови екстремуму. Розділи, присвячені необхідним умовам екстремуму (і достатніх умов екстремуму), стали розроблятися в 18 столітті Л. Ейлером, Ж. Лагранжем і А. Лежандром. Починаючи з 1730-х років Ейлер займався проблемою про умови екстремуму в задачах варіаційного обчислення. Таким умовою для найпростіших завдань варіаційного числення (найпростішими називаються завдання про екстремуми функціоналів J при фіксованих граничних умовах) виявилася здійсненність на кривій х, підозрюваної на екстремум, диференціального рівняння 2-го порядку

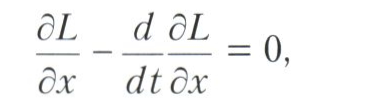
що отримав назву Ейлера рівняння. У важливому окремому випадку (він пов'язаний з так званим гармонійним осцилятором), коли L = mх2 - kx2, рівняння Ейлера набуває вигляду

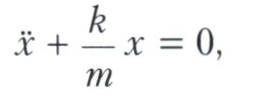
і граничні умови, взагалі кажучи, дозволяють однозначно визначити синусоїду (рішення цього рівняння), що сполучає дві дані точки, задані крайовими умовами. Криві, що задовольняють рівняння Ейлера, називають екстремалами, а рівняння Ейлера - умовою стаціонарності. Це рівняння Л. Ейлер вивів прямим методом, замінюючи криву ламаної, т. Е. Зводячи завдання до конечномерной (з подальшим переходом до межі).

Л. Ейлер став вперше розглядати завдання з обмеженнями, а саме ізопериметричні завдання, коли інтеграл J мінімізується за умови, що деякі інші інтеграли приймають задані значення. Класична изопериметрическая завдання складається в максимізації площі, обмеженої кривою заданої довжини. Розроблені Ейлером методи дозволили одноманітно вирішити ряд завдань, цікавих для природознавства і геометрії. Серед них завдання про провисанні важкої нитки, про мінімальну поверхні обертання, а також різні варіанти класичної изопериметрической завдання. Досягнення варіаційного обчислення приводили до розуміння того, що воно може служити мовою природознавства, оскільки багато законів природи можуть бути сформульовані з використанням варіаційних принципів (дивись Можливих переміщень принцип, Найменшого дії принцип).

У 1755 році завданнями варіаційного обчислення почав займатися Ж. Лагранж. Він запропонував новий підхід до дослідження властивостей екстремальних кривих, заснований на варіюванні кривої, підозрюваної на екстремум, і виділення головної лінійної частини приросту функціоналу, тобто крива, підозрювана на екстремум, піддається малим змінам, варіюється, і вивчається питання щодо приросту функціоналу, пов'язаного з таким варіюванням.

Пізніше цими питаннями займався також Л. Ейлер, який в роботі «Елементи обчислення варіацій» (+1764) ввів терміни «варіація» і «варіаційне числення». Для багатовимірних задач варіаційного числення методом варіацій аналоги рівняння Ейлера були отримані в 1-ій половині 19 століття К. Гауссом і М. В. Остроградським.

Ж. Лагранж досліджував завдання варіаційного обчислення з обмеженнями різної природи. Для задач знаходження екстремумів функцій багатьох змінних з обмеженнями типу рівностей він став застосовувати загальний прийом, який отримав назву методу множників Лагранжа (дивись Лагранжа функція). Аналогічні прийоми Лагранж застосовував в задачах варіаційного обчислення. Метод множників Лагранжа дозволяє одноманітно виписувати необхідні умови екстремуму в різних завданнях варіаційного обчислення.

Достатні умови екстремуму. Питання про достатні умови в варіаційному численні вперше вивчав І. Бернуллі, але його робота (1718) залишалася невідомою аж до 20 століття. У 1786 році А. Лежандра знайшов необхідна умова екстремальності кривої, що складається в тому, що друга варіація д2L / д (х?) 2 неотрицательна (необхідна умова Лежандра). Гіпотеза про те, що достатня умова екстремуму є позитивність другий варіації (посилене умова Лежандра), виявилася невірною.

Проблему достатності слабкого екстремуму (коли вимірюється близькість не тільки самих функцій, але і їх похідних) дозволив К. Якобі, спираючись на ідеї У. Гамільтона, які той застосовував для задач механіки й оптики. Якобі показав, що локальних, т. Е., Що перевіряються в окремих точках умов (такі рівняння Ейлера і умова Лежандра) не може бути достатньо для екстремальності кривої.

К. Якобі ввів поняття сполученої точки екстремали варіаційної задачі. Для найпростішої завдання варіаційного обчислення сполучена точка має простий геометричний зміст: це точка перетину з екстремалами обвідної сімейства екстремалів, які мають спільну початкову точку. Відсутність сполученої точки на інтервалі від початкової до кінцевої точки - необхідна умова слабкого мінімуму (необхідна умова Якобі). Відсутність сполученої точки на полуінтервале від початкової точки до кінцевої, включаючи останню (посилене умова Якобі), спільно з рівнянням Ейлера і посиленим умовою Лежандра, досить для слабкого мінімуму екстремали.

У 19 столітті У. Гамільтону вдалося побудувати, вирушаючи від принципу Гюйгенса, теорію оптичних явищ, а К. Якобі переніс ці концепції Гамільтона на загальні завдання варіаційного обчислення, що призвело до створення теорії Гамільтона - Якобі. У цій теорії досліджуються пучки екстремалів, подібні пучків променів, і аналоги хвильових фронтів в задачах оптики. Виробляють функції, що виникають в цих завданнях, задовольняють рівнянням з приватними похідними, який отримав назву Гамільтона - Якобі рівнянь. Рішення цих рівнянь дає новий підхід до вирішення завдань варіаційного числення. При такому підході К. Вейерштрассом в 1880-і роки були знайдені умови сильного мінімуму (коли враховується близькість лише фазових координат).

Рішення проблем, пов'язаних з достатніми умовами в задачах з обмеженнями, завершилося лише до середини 20 століття, коли почав складатися новий розділ теорії екстремальних задач, що отримав назву теорії оптимального управління. Завданнями оптимального управління називаються завдання варіаційного обчислення з додатковими умовами на змінні (типу нерівностей і включень), в яких відображаються обмежені можливості впливу на керовані процеси. фундаментальне значення в теорії оптимального управління має Понтрягіна принцип максимуму; необхідні умови Ейлера, Лежандра, Якобі і Вейєрштрасса є наслідками принципу максимуму.

Створення в 20 столітті функціонального аналізу дозволило розглядати варіаційне числення та оптимальне управління як частини цього розділу математики.

Питання існування екстремуму. Теорія існування рішень задач варіаційного числення була створена в 20 столітті. Основи цієї теорії також базуються на загальних концепціях функціонального аналізу.

Алгоритми пошуку рішення. Алгоритми рішення задач варіаційного числення будуються на ідеях штрафу, прямих методах, які вигідно відрізняються завдання конечномерной, і методах вирішення рівнянь, отриманих з необхідних умов екстремуму.

Літ .: Гельфанд І. М., Фомін С. В. Варіаційне числення. М., 1961; Алексєєв В. М., Тихомиров В. М., Фомін С. В. Оптимальне управління. М., 1979; Буслаєв В. С. Лекції з варіаційного числення. Л., 1980; Васильєв Ф. П. Методи оптимізації. , 2002.

В. М. Тихомиров.