варыяцыйнага вылічэння

1. рэклама

Варыяцыйнага вылічэння, раздзел матэматыкі, у якім вывучаюцца пытанні, звязаныя з экстрэмуму інтэгральных функцыяналаў спецыяльнага віду. У найпростым выпадку гэта функцыяналам выгляду

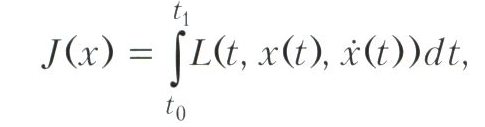
дзе L = L (t, х, у) - функцыя трох зменных (званая интегрантом).

Тут х = х (t), у = у (t) - функцыі зменнай t, t0≤t≤t1,? X (t) - вытворная функцыі х (t). Такім чынам, значэннямі аргумента функцыяналу J з'яўляюцца функцыі х аднаго пераменнага, т. Е. Варыяцыйнага вылічэння - раздзел бесконечномерного аналізу, які атрымаў у 20 стагоддзі назву функцыянальнага аналізу. З іншага боку, варыяцыйнага вылічэння з'яўляецца раздзелам тэорыі экстрэмальных задач.

Першыя задачы варыяцыйнага вылічэння. Гістарычна першай задачай варыяцыйнага вылічэння была задача аб брахистохроне, якая складаецца ў знаходжанні крывой найхутчэйшага спуску, якая злучае дзве зададзеныя кропкі (ці, інакш кажучы, у знаходжанні формы жолаба, які злучае дзве кропкі, спускаючыся па якім без трэння пад дзеяннем сілы цяжару, цела завяршае рух за самы кароткі час). Задачу аб брахистохроне можна сфармуляваць як задачу варыяцыйнага вылічэння аб мінімізацыі інтэграла

рэклама

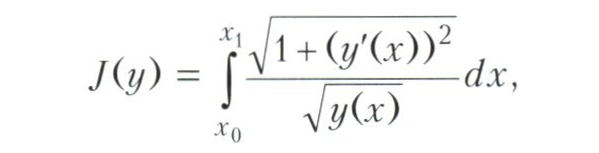
дзе ў (х) - форма жолаба і (х0, у (х0)), (х1, у (х1)) - замацаваныя пачатковая і канчатковая пункту жолаба. Гэтая задача была прапанавана І. Бярнулі у 1696 годзе як выклік матэматыкам (ён абвясціў, што ведае яе рашэнне). Выклік быў прыняты, і задача была вырашана найбуйнейшымі навукоўцамі таго часу - Я. Бярнулі, Г. Лейбніцам, французскім навукоўцам Г. Лопиталем і І. Ньютанам. Гэтыя рашэнні намецілі многія напрамкі будучай агульнай тэорыі. І. Бярнулі зыходзіў з оптыка-механічнай аналогіі, Я. Бярнулі ужыў прынцып Гюйгенса (глядзі Гюйгенса - Фрэнэля прынцып), Лейбніц вырашыў задачу, замяняючы крывую ламанымі, заклаўшы тым самым аснову прамым метадам ў варыяцыйнага вылічэння.

У варыяцыйнага вылічэння можна вылучыць раздзелы, прысвечаныя неабходным умовам экстрэмуму, дастатковым умовам экстрэмуму, пытаннях існавання экстрэмуму і алгарытмам пошуку рашэнняў.

Неабходныя ўмовы экстрэмуму. Раздзелы, прысвечаныя неабходным умовам экстрэмуму (і дастатковым умовам экстрэмуму), сталі распрацоўвацца ў 18 стагоддзі Л. Эйлера, Ж. Лагранжа і А. Лежандра. Пачынаючы з 1730-х гадоў Эйлер займаўся праблемай пра ўмовы экстрэмуму ў задачах варыяцыйнага вылічэння. Такой умовай для найпростых задач варыяцыйнага вылічэння (найпростымі называюцца задачы аб экстрэмуму функцыяналаў J пры фіксаваных межавых умовах) апынулася выканальнасць на крывой х, падазраванай на экстрэмуму, дыферэнцыяльнага раўнання 2-га парадку

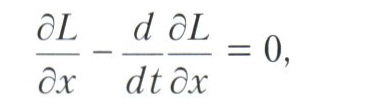
які атрымаў назву Эйлера ўраўненні. У важным прыватным выпадку (ён звязаны з так званым гарманічным асцылятар), калі L = mх2 - kx2, раўнанне Эйлера прымае выгляд

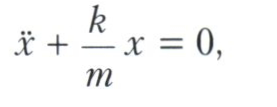
і межавыя ўмовы, наогул кажучы, дазваляюць адназначна вызначыць сінусоіду (рашэнне гэтага раўнання), якая злучае дзве дадзеныя пункту, зададзеныя краявымі ўмовамі. Крывыя, якія задавальняюць раўнанню Эйлера, называюць экстрэмалаў, а раўнанне Эйлера - умовай стацыянарнага. Гэта раўнанне Л. Эйлер вывеў прамым метадам, замяняючы крывую ламанай, т. Е. Зводзячы задачу да канечнамернае (з наступным пераходам да мяжы).

Л. Эйлер стаў ўпершыню разглядаць задачы з абмежаваннямі, а менавіта изопериметрические задачы, калі інтэграл J мінімізуецца пры ўмове, што некаторыя іншыя інтэгралы прымаюць зададзеныя значэнні. класічная изопериметрическая задача складаецца ў максімізацыі плошчы, абмежаванай крывой зададзенай даўжыні. Распрацаваныя Эйлера метады дазволілі аднастайна вырашыць шэраг задач, цікавых для прыродазнаўства і геаметрыі. Сярод іх задачы аб правісання цяжкай ніткі, аб мінімальнай паверхні кручэння, а таксама розныя варыянты класічнай изопериметрической задачы. Дасягнення варыяцыйнага вылічэння прыводзілі да разумення таго, што яно можа служыць мовай прыродазнаўства, паколькі многія законы прыроды могуць быць сфармуляваны з выкарыстаннем варыяцыйная прынцыпаў (глядзі Магчымых перасоўванняў прынцып, Найменшага дзеянні прынцып).

У 1755 годзе задачамі варыяцыйнага вылічэння пачаў займацца Ж. Лагранжа. Ён прапанаваў новы падыход да даследавання уласцівасцяў экстрэмальных крывых, заснаваны на вар'іраванні крывой, падазраванай на экстрэмуму, і выдзяленні галоўнай лінейнай часткі прырашчэння функцыяналу, то ёсць крывая, падазраваная на экстрэмуму, падвяргаецца малым зменам, вар'іруецца, і вывучаецца пытанне аб прырашчэння функцыяналу, звязанага з такім вар'іраваннем.

Пазней гэтымі пытаннямі займаўся таксама Л. Эйлер, які ў працы «Элементы вылічэння варыяцый» (1764) увёў тэрміны «варыяцыя» і «варыяцыйнага вылічэння". Для шматмерных задач варыяцыйнага вылічэння метадам варыяцый аналагі ўраўненні Эйлера былі атрыманы ў 1-й палове 19 стагоддзя К. Гаўса і М. В. Остроградского.

Ж. Лагранжа даследаваў задачы варыяцыйнага вылічэння з абмежаваннямі рознай прыроды. Для задач знаходжання экстрэмуму функцый многіх зменных з абмежаваннямі тыпу роўнасцяў ён стаў ужываць агульны прыём, які атрымаў назву метаду множнікаў Лагранжа (глядзі Лагранжа функцыя). Аналагічныя прыёмы Лагранжа ўжываў у задачах варыяцыйнага вылічэння. Метад множнікаў Лагранжа дазваляе аднастайна выпісваць неабходныя ўмовы экстрэмуму ў розных задачах варыяцыйнага вылічэння.

Дастатковыя ўмовы экстрэмуму. Пытанне аб дастатковых умовах у варыяцыйнага вылічэння ўпершыню вывучаў І. Бярнулі, але яго праца (1718) заставалася невядомай аж да 20 стагоддзя. У 1786 году А. Лежандр знайшоў неабходная ўмова экстрэмальнасці крывой, якое складаецца ў тым, што другая варыяцыя д2L / в (х?) 2 неадмоўнага (неабходная ўмова Лежандра). Гіпотэза аб тым, што дастатковай умовай экстрэмуму з'яўляецца станоўча другі варыяцыі (ўзмоцненае ўмова Лежандра), апынулася няслушнай.

Праблему дастатковасці слабога экстрэмуму (калі вымяраецца блізкасць не толькі саміх функцый, але і іх вытворных) дазволіў К. Якобі, абапіраючыся на ідэі У. Гамільтана, якія той ўжываў для задач механікі і оптыкі. Якобі паказаў, што лакальных, т. Е. Правяраемых ў асобных кропках умоў (такія раўнанне Эйлера і ўмова Лежандра) не можа быць дастаткова для экстрэмальнасці крывой.

К. Якобі увёў паняцце спалучаныя пункту экстрэмал варыяцыйнай задачы. Для найпростай задачы варыяцыйнага вылічэння спалучаная кропка мае просты геаметрычны сэнс: гэта кропка перасячэння з экстрэмалаў абгінаючай сямейства экстрэмалаў, якія маюць агульную пачатковую кропку. Адсутнасць спалучаныя кропкі на інтэрвале ад пачатковай да канчатковай кропкі - неабходная ўмова слабога мінімуму (неабходная ўмова Якобі). Адсутнасць спалучаныя кропкі на полуинтервале ад пачатковай кропкі да канчатковай, уключаючы апошнюю (ўзмоцненае ўмова Якобі), сумесна з раўнаннем Эйлера і ўзмоцненым умовай Лежандра, дастаткова для слабога мінімуму экстрэмал.

У 19 стагоддзі У. Гамільтану ўдалося пабудаваць, адпраўляючыся ад прынцыпу Гюйгенса, тэорыю аптычных з'яў, а К. Якобі перанёс гэтыя канцэпцыі Гамільтана на агульныя задачы варыяцыйнага вылічэння, што прывяло да стварэння тэорыі Гамільтана - Якобі. У гэтай тэорыі даследуюцца пучкі экстрэмалаў, падобныя пучкам прамянёў, і аналагі хвалевых франтоў у задачах оптыкі. Якія вырабляюць функцыі, якія ўзнікаюць у гэтых задачах, задавальняюць раўнаннях з прыватнымі вытворнымі, якія атрымалі назву Гамільтана - Якобі раўнанняў. Вырашэнне гэтых раўнанняў дае новы падыход да вырашэння задач варыяцыйнага вылічэння. Пры такім падыходзе К. Веерштрас ў 1880-я гады былі знойдзеныя ўмовы моцнага мінімуму (калі ўлічваецца блізкасць толькі фазавых каардынатаў).

Рашэнне праблем, звязаных з дастатковымі ўмовамі ў задачах з абмежаваннямі, завяршылася толькі да сярэдзіны 20 стагоддзя, калі пачаў складвацца новы раздзел тэорыі экстрэмальных задач, які атрымаў назву тэорыі аптымальнага кіравання. Задачамі аптымальнага кіравання называюцца задачы варыяцыйнага вылічэння з дадатковымі ўмовамі на зменныя (тыпу няроўнасцей і уключэнняў), у якіх адлюстроўваюцца абмежаваныя магчымасці ўздзеяння на кіраваныя працэсы. фундаментальнае значэнне у тэорыі аптымальнага кіравання мае Понтрягина прынцып максімуму; неабходныя ўмовы Эйлера, Лежандра, Якобі і Веерштрас з'яўляюцца следствамі прынцыпу максімуму.

Стварэнне ў 20 стагоддзі функцыянальнага аналізу дазволіла разглядаць варыяцыйнага вылічэння і аптымальнае кіраванне як часткі гэтага падзелу матэматыкі.

Пытанні існавання экстрэмуму. Тэорыя існавання рашэнняў задач варыяцыйнага вылічэння была створана ў 20 стагоддзі. Асновы гэтай тэорыі таксама грунтуюцца на агульных канцэпцыях функцыянальнага аналізу.

Алгарытмы пошуку рашэння. Алгарытмы рашэння задач варыяцыйнага вылічэння будуюцца на ідэях штрафу, прамых метадах, якія замяняюць задачу канечнамернае, і метадах рашэння раўнанняў, атрыманых з неабходных умоў экстрэмуму.

Літ .: Гельфанд І. М., Фамін С. В. варыяцыйнага вылічэння. М., 1961 г.; Аляксееў В. М., Ціхаміраў В. М., Фамін С. В. Аптымальнае кіраванне. М. 1979; Буслаев В. С. Лекцыі па варыяцыйнага вылічэння. Л., 1980; Васільеў Ф. П. Метады аптымізацыі. М. 2002.

В. М. Ціхаміраў.